Simulación del Modelo SIR

El modelo matemático SIR cuyas siglas provienen de Susceptibles-Infectados-Recuperados se utiliza para representar y estudiar matemáticamente la evolución de enfermedades infecciosas, como por ejemplo la pandemia causada por el virus de la COVID-19. En este modelo la población se divide en tres grupos distintos:

• Susceptibles: sujetos que no han contraído el virus y pueden contagiarse por el mismo.
• Infectados: sujetos que han contraído el virus.
• Recuperados: sujetos que han contraído el virus y se han curado. En este grupo también se incluyen los fallecidos aunque no hayan conseguido superar la enfermedad. Es por ello que en inglés es común denominar este grupo por removed.

En los modelos más simples suponemos que una persona que ha contraído el virus y se ha curado ha desarrollado anticuerpos y no vuelve a contagiarse. En el caso de sujetos que fueran inmunes al virus, por ejemplo por razones genéticas, estos se incluirían directamente en el grupo de los recuperados.

La cantidad de individuos susceptibles, infectados y recuperados variará con el paso del tiempo, de modo que tenemos tres funciones en las que la variable independiente es el tiempo, \(\textstyle S(t), I(t)\) y \(\textstyle R(t)\).

Algunas hipótesis que añadimos a nuestro modelo son:

• La población es constante, es decir \(\textstyle N=S(T)+I(t)+R(t)\). Esta hipótesis establece que la epidemia no se extiende durante el suficiente tiempo como para que la cantidad de individuos en la población varíe. Entre otras cosas ignoramos los nuevos nacimientos, la inmigración y los fallecimientos por causas ajenas al virus.
• Todos los individuos tienen la misma probabilidad de infectarse.
• Suponemos que la posibilidad de infectarse por el virus es proporcional al número de contactos que hay entre personas infectas y personas susceptibles, y esta proporcionalidad no varía con el tiempo.
• Los individuos que dejan de ser susceptibles es porque han sido infectados.
• Los contactos entre los distintos individuos de la población se producen de forma aleatoria y uniforme.

Estas hipótesis se representan con el siguiente diagrama donde se establece que los individuos solamente pueden desplazarse de la categoría de susceptibles a infectados y de la de infectados a recuperados.

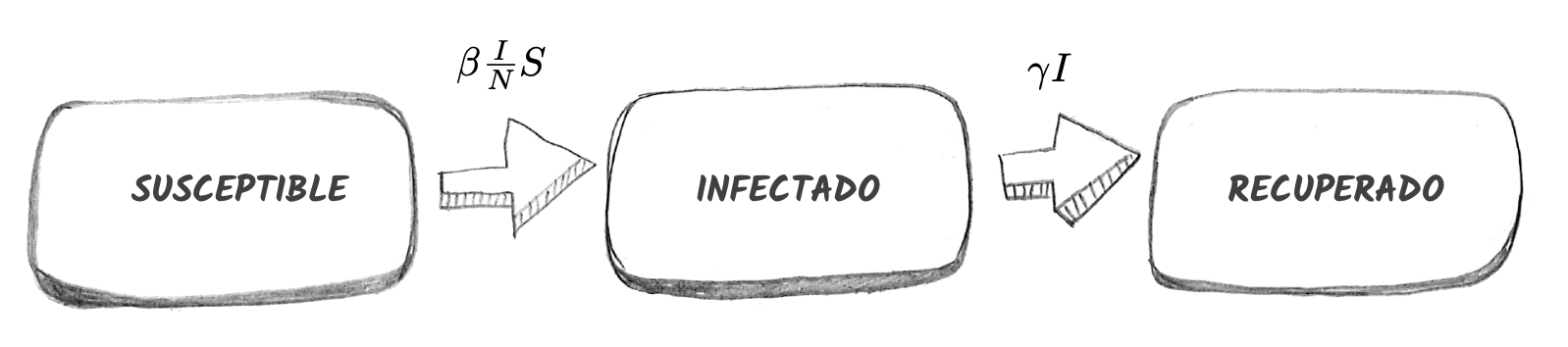
Matemáticamente el modelo viene representado por el siguiente sistema de ecuaciones diferenciales ordinarias:

\[\begin{cases} \frac{dS}{dt}=-\beta I\frac{S}{N}\\ \frac{dI}{dt}=\beta I\frac{S}{N}-\gamma I\\ \frac{dR}{dt}=\gamma I \end{cases}\]

El siguiente applet interactivo nos representa las soluciones \(\textstyle S(t), I(t)\) y \(\textstyle R(t)\) del sistema de ecuaciones diferenciales depeniendo de la tasa de transmisión \(\textstyle \beta\) y la tasa de recuperación \(\textstyle \gamma=\frac{1}{\text{tiempo medio de recuperación}}\). En este caso se asume que el tamaño de la población es \(\textstyle N=1\) y por tanto las funciones \(\textstyle S(t), I(t)\) y \(\textstyle R(t)\) representan el porcentaje de la población Susceptibles, Infectado y Recuperado.