Instrucciones:

• Descarga y monta el siguiente sistema de coordenadas.
• Coloca las vías de madera sobre el papel cuadriculado siguiendo las indicaciones que se dan en la gráfica: La parte superior del recorrido marcado por las vías sigue la ecuación $$f(t)=\sqrt{121-t^2}.$$
• Desplaza el tren por las vías en sentido antihorario.

• El principio de la vía marcada con rojo corresponde a los valores $$\textstyle\left(t,f(t)\right)=\left(\frac{11}{\sqrt{2}},\frac{11}{\sqrt{2}}\right).$$ Calcula la derivada de la función $$\textstyle f$$ en este punto.
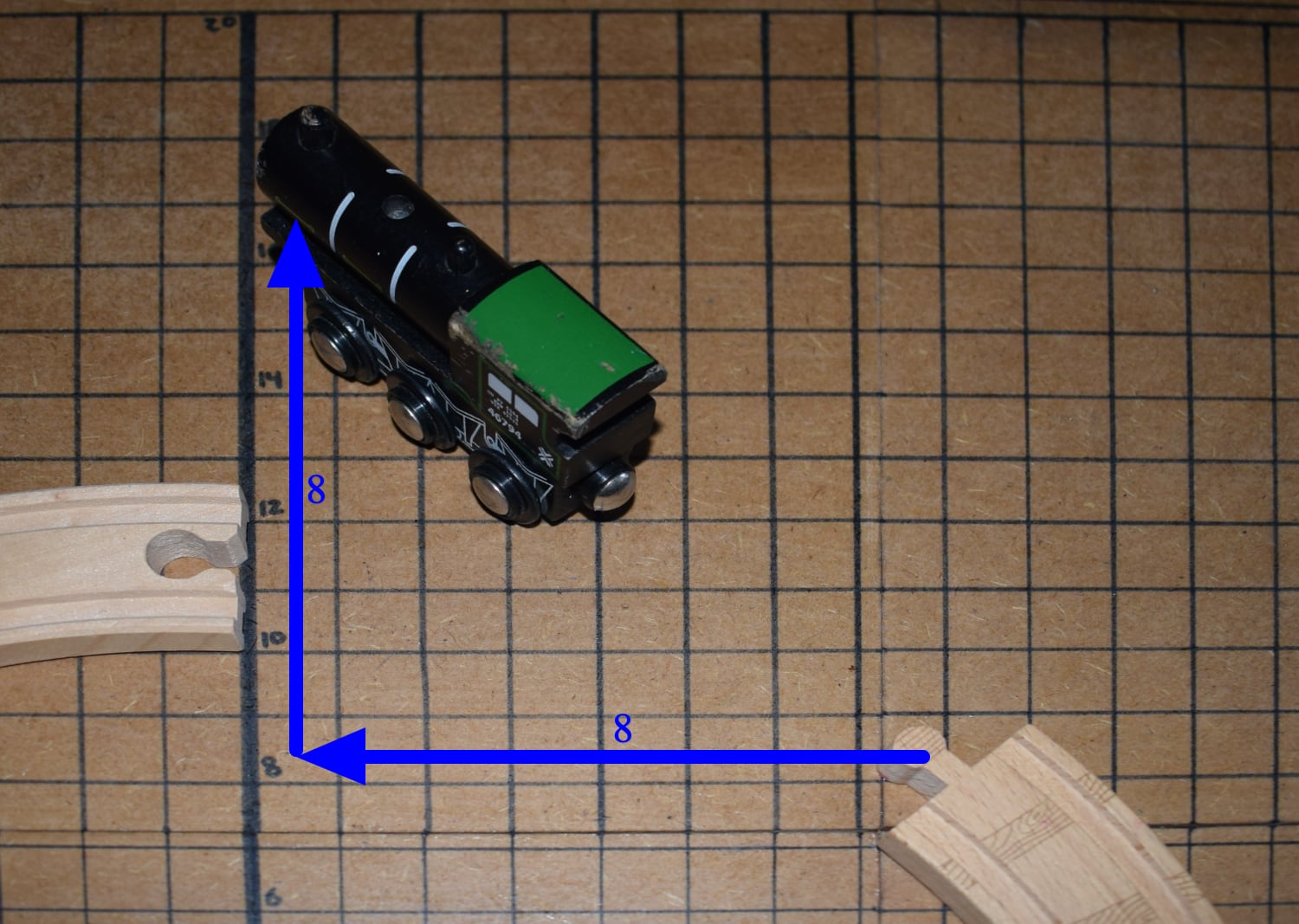
• Elimina la via marcada de color rojo y empujar el tren con suficiente fuerza para que siga su transcurso natural al pasar el punto marcado de color rojo. El video se añadirá en breve.
• Calcula el desplazamiento horizontal realizado por el tren desde el punto marcado hasta el punto en el que este se ha detenido. Nota que horizontalmente el tren se desplazará hacia la derecha produciendo un desplazamiento positivo, mientras que verticalmente el tren se desplazará hacia abajo produciendo un desplazamiento negativo. El cociente dado por $$\frac{\text{desplazamiento vertical}}{\text{desplazamiento horizontal}}$$ ha de coincidir con el valor de la derivada en el punto $$\textstyle t=\frac{11}{\sqrt{2}}.$$