La caja de palomitas del cine
Materiales:
- Hojas tamaño A4.
- Cinta adhesiva.
- Una bolsa grande de palomitas cocinadas.
Instrucciones:
- Marca en una hoja A4 cuatro cuadrados en las esquinas utilizando la altura que crees que es óptima para la construcción de la caja de palomitas. Anota el valor seleccionado de la altura (los cuatro cuadrados tienen la misma).
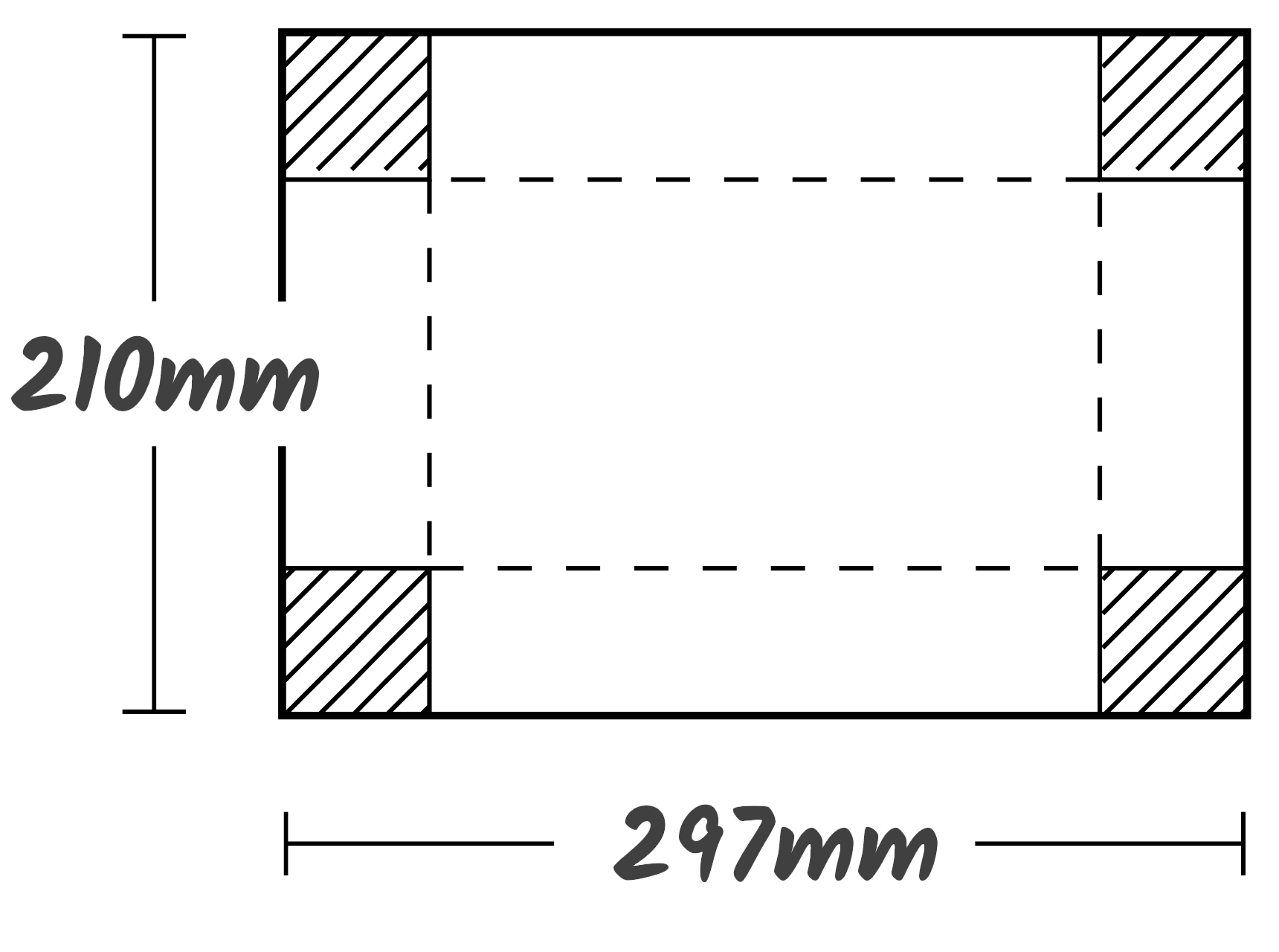
- Recorta esta altura y monta la caja de palomitas doblando la hoja por la línea discontinua y pegando las paredes de la caja con la cinta adhesiva.
- Repite los pasos anteriores para montar varias cajas de distintos tamaños.
- Compara la capacidad de las distintas cajas. Para comparar la capacidad de las cajas de palomitas, rellenamos la caja con palomitas hasta cubrirla por completo, pero sin que las palomitas sobresalgan de la misma. Las palomitas pueden romperse y apretarse para que quepan más dentro de la caja. A continuación vuelca las palomitas de una caja llena en otra vacía. Si caben todas las palomitas dentro de esta segunda caja y todavía queda espacio para añadir más palomitas, quiere decir que esta tiene mayor capacidad y por tanto su volumen está mas optimizado.



Esta actividad resulta más exacta si en lugar de utilizar palomitas cocinadas se utiliza un material que rellene mejor la caja como pueden ser los granos de palomitas o arroz. Pero siempre es más divertido y provechoso el conocimiento cuando se digiere.
Para obtener la caja óptima.
Para estudiar cuál es la caja con mayor capacidad hemos de considerar la función que nos da el volumen de la caja dependiendo de las dimensiones del corte que realizamos. En este caso es altura por anchura por profundidad en milímetros, \(Vol(x)=(297-2x)\cdot(210-2x)\cdot x = 4 x^3 - 1014x^2 + 62370x.\)
En nuestro contexto esta función solo tiene sentido para valores de \(\textstyle x\) entre 0 y 105 porque no podemos hacer cortes con longitudes negativas ni que sean más grandes que la mitad de la anchura de la hoja A4.
Para utilizar el método del intervalo cerrado, lo primero que tenemos que hacer es encontrar los puntos críticos de la función. La derivada de la función volumen es: \(Vol'(x)=12x^{2}-2028x+62370.\)
Utilizando la fórmula que nos da la solución para una ecuación de segundo grado \(\textstyle \frac{-b\pm\sqrt{b^2-4ac}}{2a}\) con \(\textstyle a=12, b=-2028\) y \(\textstyle c=62370\) obtenemos que los puntos críticos, en los que \(\textstyle Vol'(x)\) es igual a cero, son \(\textstyle \frac{2028\pm\sqrt{1119024}}{24}\), aproximadamente \(\textstyle 40.42\) y \(\textstyle 128.58\) milímetros. Es importante señalar que el segundo de los valores no nos sirve porque es mayor que 105.
Evaluando \(\textstyle Vol(x)\) en \(\textstyle x=0\), \(\textstyle x=40.423\) y en \(\textstyle x=105\) obtenemos: \(Vol(0)=0, Vol(40.423)=1128425, Vol(105)=0,\)
por lo que el mayor volumen que podemos obtener es \(\textstyle 1\,128\,425\) milímetros cúbicos cuando el corte que realizamos es de \(\textstyle 40.42\) milímetros aproximadamente.


